Opis modelu STOCH-SEIR

Założenia modelu

Model SEIR w wersji bayesowskiej zakłada istnienie pięciu grup w populacji:

S: grupa osób, która jest narażona na zakażenie;
E: grupa osób, która uległa zakażeniu, ale nie zaraża. W sytuacji modelowej osoba należy do tej grupy do momentu, w którym nie jest w stanie jeszcze zarażać innych osób;
ID: grupa osób, które zarażają inne osoby w populacji i zostaną w przyszłości zdiagnozowane;
IU: grupa osób, które zarażają inne osoby w populacji i nie zostaną w przyszłości zdiagnozowane;
R: grupa osób, które zostały zdiagnozowane i przestały zarażać, np. w wyniku izolacji czy wyzdrowienia.
U: grupa osób, które nie zostały zdiagnozowane, ale przestały zarażać, np. w wyniku wyzdrowienia lub samoizolacji

Dodatkowo w modelu bayesowskim grupy populacji związane są z danymi:

T: dzienne liczby wykonanych testów
Ts: lokalnie uśrednione dzienne liczby testów (w tygodniowym oknie)
P: dzienne liczby zdiagnozowanych przypadków
Z: dzienne liczby zgonów

Parametry modelu

Kluczowe sześć parametrów modelu:

β_D: jest to częstość, z jaką następuje zarażenie osoby podatnej przez osoby z ID. Parametr ten wiąże dwa czynniki: prawdopodobieństwo zarażenia przy bezpośrednim kontakcie z zakażonym oraz średnią liczbę kontaktów podatnego z zakażonym w jednostce czasu. Ze względu na stopniowo wprowadzane restrykcje parametr ten w modelu przyjmuje różne wartości w zależności od czasu. Przyjęto dwie zmiany wartości parametru 12.03 (zamknięcie szkół), 25.03 (wprowadzenie znacznych ograniczeń w kontaktach społecznych);
β_U: jest to częstość, z jaką następuje zarażenie osoby podatnej przez osoby z IU. Parametr ten wiąże dwa czynniki: prawdopodobieństwo zarażenia przy bezpośrednim kontakcie z zakażonym oraz średnią liczbę kontaktów podatnego z zakażonym w jednostce czasu. Ze względu na stopniowo wprowadzane restrykcje parametr ten w modelu przyjmuje różne wartości w zależności od czasu. Przyjęto dwie zmiany wartości parametru 12.03 (zamknięcie szkół), 25.03 (wprowadzenie znacznych ograniczeń w kontaktach społecznych);
σ^-1: średni czas, po którym następuje przejście z grupy E do I. Parametr jest interpretowany, jako czas związany z okresem inkubacji wirusa;
γ^-1: średni czas, po którym następuje przejście z grupy IU do U. Jest to średni czas trwania zaraźliwości u osób niezdiagnozowanych , tj. czas potrzebny na wyzdrowienie osoby;
δ: frakcja osób zakażonych, która będzie testowana w danej chwili czasul
η: frakcja zdiagnozowanych

Przejścia pomiędzy stanami

Z S do E, czyli przejście z grupy narażonych do zakażonych, jeszcze nie zarażających, wynosi β_D · S · ID + β_U · S · IU.
Z E do ID, czyli okres inkubacji wynosi η · σ · E.
Z E do IU, czyli okres inkubacji wynosi (1 - η) · σ · E.
Z ID do R, czyli zdiagnozowane przypadki ρ = δ · ID · T / Ts + (I · DT) / (N - R - U) odpowiada to sytuacji gdy δ spośród zakażonych jest diagnozowana, skorygowane o nietypową liczbę testów danego dnia, dodatkowo losowe osoby z populacji z frakcją odpowiadająca liczbie zakażonych. Zakładamy, że do R przechodzi min(ρ, 0.8 · T), gdzie 0.8 jest ustalona autorytarnie maksymalnym odsetkiem wyników pozytywnych jednego dnia.
Z IU do U przechodzi γ · I.

Model danych

Zakładamy, że P ~ Bin(ρ / T, T), gdzie ρ opisane powyżej. Oznacza to, że liczba osób zdiagnozowanych ma rozkład dwumianowy o wartości oczekiwanej równej przepływowi z I do R i liczbie prób równej faktycznie wykonanym testom.
Zakładamy, że dzienna liczba zgonów Z ma rozkład Poissona.
Z ~ Poiss(Θ), gdzie Θ(t)= η · σ · ifr · (E(t - 28) + E(t - 13) + ... + E(t - 7))/21. Przyjmujemy, że do śmierci dochodzi najczęściej od 7 do 28 dni od zakażenia. Na podstawie danych oszacowany współczynnik śmiertelności wśród zdiagnozowanych przypadków na 4,5%.

Sposób estymacji parametrów

Dla wyżej opisanego modelu parametry β, γ, η, σ, δ zostały opisane rozkładem a priori gamma z hiperparametrami dobranymi z literatury, lub z wcześniejszych wniosków z deterministycznego modelu SEIR. Dodatkowo dla parametrów δ, η , zadano rozkład a priori jednostajny na odcinku [0,1]. Dla tak wyprowadzonego modelu rozkład a posteriori parametrów został wyznaczony za pomocą metody Monte Carlo (Algorytm Metropolisa wewnątrz próbnika Gibbsa). Końcowe estymatory parametrów zostały wyznaczone przez wartości oczekiwane rozkładu a posteriori natomiast przedziały ufności za pomocą kwantyli tego rozkładu. (Wyznaczono estymatory bayesowskie przy kwadratowej funkcji straty)

Prognozowanie

Po wyestymowaniu parametrów do prognozowania potrzebne jest określenie liczby testów wykonanych w przyszłości. W tym celu przybliżono wzrost liczby testów na podstawie dotychczasowych danych. Zależność pomiędzy liczbą testów a czasem została modelowana przez model liniowy po transformacji Boxa-Coxa. Dodatkowo, założyliśmy, że liczba testów jednego dnia nie może przekroczyć możliwości systemu (25 tys. dotychczas). Dodatkowo przyjęto logarytmiczny wzrost δ odzwierciedlający zwiększenie wykrywania przypadków wraz ze wzrostem liczby testów. Funkcja logarytmiczna jest dobrana tak, aby początkowo następował liniowy wzrost wykrywalności i dynamika wzrostu spadała po osiągnięciu 2δ. Przedziały ufności dla prognoz otrzymano przez uśrednienie trajektorii w przyszłości względem rozkładu a posteriori.

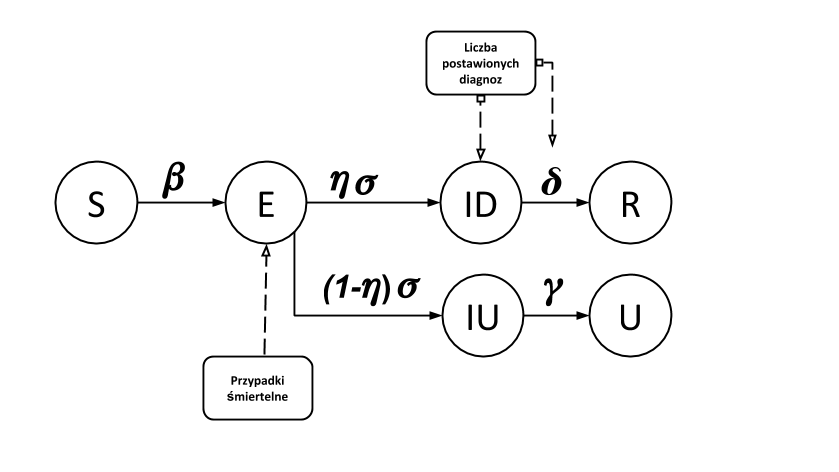
Rysunek 1. Schematyczne przedstawienie modelu stochSEIR. Schemat przedstawia znaczenie poszczególnych stanów względem opisu klinicznego zakażonego oraz wskazuje jakie dane mogą być użyte do kalibracji modelu, jak również wyprowadzania predykcji.

Lista parametrów rozkładów a priori

E(β₁) = 0.4
sd(β₁) = 0.1
E(β₂) = 0.345
sd(β₂) = 0.1
E(β₃) = 0.29
sd(β₃) = 0.1
E(γ₁) = 0.11
sd(γ₁) = 0.1
E(σ₁) = 0.4
sd(σ₁) = 0.1

Lista parametrów rozkładów a posteriori

Parametry a posteriori	β₁		β₂		β₃		β₄		γ^-1	σ^-1	δ	η₁ (η₂)
Parametry a posteriori	β_{1, D}	β_{1, U}	β_{2, D}	β_{2, U}	β_{3, D}	β_{3, U}	β_{4, D}	β_{4, U}	γ^-1	σ^-1	δ	η₁ (η₂)
02-05-2020	1.1 (0.782 - 1.37)		0.642 (0.569 - 0.715)		0.112 (0.0669 - 0.201)				33.3 (11.6 - 162)	5.56 (3.25 - 7.87)	0.0775 (0.0575 - 0.107)	0.0004 (0.000285 - 0.000618)
07-05-2020	1.14 (0.782 - 1.45)		0.661 (0.591 - 0.793)		0.11 (0.0607 - 0.208)				33.9 (11.3 - 216)	5.68 (3.19 - 9.26)	0.0784 ( 0.0571 - 0.106)	0.000382 (0.000271 - 0.000585)
09-05-2020	1.18 (0.772 - 1.56)		0.648 (0.588 - 0.705)		0.101 (0.0572 - 0.177)				34.4 (12.2 - 207)	5.85 (3.14 - 8.4)	0.071 (0.0519 - 0.0922)	0.000353 (0.000257 - 0.000541)
15-05-2020	1.21 (0.977 - 1.77)	2.16 (2.16 - 2.16)	0.504 (0.466 - 0.608)	0.616 (0.554 - 0.67)	0.0587 (0.0465 - 0.111)	0.118 (0.0885 - 0.15)			8.4 (6.45 - 10.9)	5.95 (5.68 - 6.21)	0.0634 (0.0493 - 0.122)	0.538 (0.217 - 0.732)
17-05-2020	1.31 (0.97 - 1.95)	1.5 (1.27 - 2.04)	0.607 (0.517 - 0.679)	0.535 (0.391 - 0.662)	0.047 (0.033 - 0.058)	0.228 (0.0999 - 0.356)	0.104 (0.066 - 0.146)	0.17 (0.0728 - 0.302)	5.08 (3.73 - 11.2)	4.67 (3.5 - 6.33)	0.0652 (0.0557 - 0.0778)	0.494 (0.3865 - 0.5)
20-05-2020	1.06 (0.641 - 1.76)	2.28 (1.87 - 2.55)	0.592 (0.509 - 0.706)	0.642 (0.541 - 0.766)	0.0667 (0.0456 - 0.0897)	0.0978 (0.0826 - 0.112)	0.1 (0.0633 - 0.148)	0.106 (0.0585 - 0.16)	9.8 (8.2 - 12.8)	6.58 (5.59 - 7.52)	0.0704 (0.0611 - 0.0867)	0.4765 (0.3255 - 0.5)
23-05-2020	1.52 (1.22 - 1.73)	1.58 (1.34 - 2.09)	0.754 (0.661 - 0.941)	0.644 (0.548 - 0.73)	0.0941 (0.0733 - 0.111)	0.128 (0.0886 - 0.163)	0.136 (0.09 - 0.229)	0.142 (0.0639 - 0.202)	7.58 (6.41 - 11.6)	6.54 (5.78 - 7.52)	0.0951 (0.0827 - 0.117)	0.472 (0.273 - 0.5)
27-05-2020	1.24 (0.926 - 1.6)	1.56 (1.37 - 1.77)	0.616 (0.551 - 0.681)	0.571 (0.51 - 0.616)	0.0638 (0.0501 - 0.0787)	0.114 (0.0904 - 0.132)	0.101 (0.0672 - 0.136)	0.107 (0.0515 - 0.157)	10.5 (8.2 - 16.7)	5.81 (5.29 - 6.67)	0.0826 (0.0764 - 0.0924)	0.498 (0.4995 - 0.5)
29-05-2020	1.29 (0.757 - 2.88)	2.1 (1.87 - 2.32)	0.778 (0.642 - 0.909)	0.619 (0.534 - 0.694)	0.0891 (0.0704 - 0.117)	0.111 (0.0753 - 0.147)	0.141 (0.0874 - 0.192)	0.0807 (0.0345 - 0.146)	8.85 (7.19 - 11.6)	7.19 (6.67 - 7.81)	0.0897 (0.0736 - 0.108)	0.464 (0.291 - 0.5)
05-06-2020	1.01 (0.82 - 1.56)	1.8 (1.67 - 1.94)	0.723 (0.539 - 0.798)	0.485 (0.401 - 0.574)	0.0795 (0.0612 - 0.0951)	0.118 (0.103 - 0.144)	0.138 (0.11 - 0.166)	0.0574 (0.0306 - 0.0839)	9.62 (7.87 - 12.1)	5.88 (5.65 - 6.06)	0.0917 (0.0834 - 0.109)	0.4765 (0.324 - 0.5)
07-06-2020	0.742 (0.572 - 0.969)	1.92 (1.71 - 2.08)	0.797 (0.715 - 1.01)	0.53 (0.474 - 0.569)	0.0782 (0.0615 - 0.0978)	0.127 (0.108 - 0.154)	0.0699 (0.0354 - 0.0988)	0.0574 (0.0306 - 0.0839)	8.2 (6.67 - 9.62)	5.46 (5.21 - 5.75)	0.0913 (0.0862 - 0.101)	0.392 (0.2575 - 0.5)
11-06-2020	1.05 (0.781 - 1.45)	1.63 (1.51 - 1.76)	0.755 (0.67 - 0.931)	0.472 (0.443 - 0.516)	0.0829 (0.0511 - 0.114)	0.112 (0.0958 - 0.124)	0.163 (0.121 - 0.212)	0.0779 (0.0598 - 0.115)	8.77 (7.81 - 10.5)	4.78 (4.5 - 5.35)	0.0863 (0.0816 - 0.0918)	0.3555 (0.2665 - 0.4285)
15-06-2020	0.792 (0.633 - 1.1)	1.87 (1.61 - 2.04)	0.675 (0.566 - 0.806)	0.575 (0.515 - 0.639)	0.0623 (0.045 - 0.0743)	0.136 (0.121 - 0.163)	0.147 (0.13 - 0.176)	0.071 (0.0549 - 0.0883)	9.17 (8.26 - 10.3)	5.62 (5.1 - 5.95)	0.09 (0.0816 - 0.098)	0.458 (0.316 - 0.5)
18-06-2020	0.822 (0.678 - 1.09)	1.54 (1.24 - 1.77)	0.642 (0.575 - 0.72)	0.592 (0.549 - 0.668)	0.0883 (0.0555 - 0.105)	0.129 (0.115 - 0.147)	0.135 (0.111 - 0.172)	0.0973 (0.0726 - 0.131)	8.06 (6.54 - 10.2)	4.93 (4.15 - 5.75)	0.095 (0.0889 - 0.1)	0.467 (0.303 - 0.5)
24-06-2020	1.33 (1.02 - 1.89)	1.83 (1.73 - 1.94)	0.67 (0.625 - 0.717)	0.535 (0.513 - 0.575)	0.0947 (0.0741 - 0.113)	0.105 (0.0974 - 0.112)	0.146 (0.126 - 0.158)	0.0754 (0.0656 - 0.0857)	9.52 (8.4 - 10.9)	5.46 (5.24 - 5.65)	0.0878 (0.0811 - 0.094)	0.319 (0.27 - 0.3495)
01-07-2020	1.14 (1.12 - 1.17)	1.82 (1.8 - 1.84)	0.927 (0.916 - 0.965)	0.489 (0.482 - 0.5)	0.0801 (0.076 - 0.0828)	0.118 (0.117 - 0.12)	0.17 (0.145 - 0.179)	0.0692 (0.0644 - 0.0778)	9.43 (9.35 - 9.43)	5.35 (5.32 - 5.41)	0.093 (0.0892 - 0.0944)	0.2795 (0.2725 - 0.283)
22-08-2020	1.23 (1.23 - 1.26)	1.78 (1.77- 1.78)	0.897 (0.893 - 0.898)	0.486 (0.479 - 0.488)	0.0804 (0.0803 - 0.0811)	0.111 (0.111 - 0.111)	0.228 (0.205 - 0.245)	0.0839 (0.0743 - 0.0985)	9.62 (9.62 - 9.62)	5.78 (5.78 - 5.78)	0.0988 (0.0986 - 0.0989)	0.3675 (0.3665 - 0.368)
27-08-2020	1.1 (1.07 - 1.1)	1.03 (1 - 1.04)	0.00633 (0.000747 - 0.00794)	0.234 (0.231 - 0.251)	0.128 (0.126 - 0.133)	0.0451 (0.0409 - 0.048)	0.196 (0.189 - 0.218)	0.0687 (0.0546 - 0.1)	8.2 (8.2 - 8.55)	7.58 (7.52 - 7.87)	0.085 (0.0836 - 0.0854)	0.4865 (0.342 - 0.496)
03-09-2020	0.812 (0.811 - 0.816)	1.13 (1.13 - 1.14)	0.0154 (0.0143 - 0.0185)	0.209 (0.208 - 0.216)	0.105 (0.104 - 0.108)	0.0843 (0.0762 - 0.0858)	0.133 (0.126 - 0.145)	0.119 (0.109 - 0.126)	8.93 (8.93 - 9.01)	6.76 (6.76 - 6.9)	0.0904 (0.09 - 0.0906)	0.498 (0.5 - 0.05)
13-09-2020	1.14 (1.14 - 1.14)	0.641 (0.64 - 0.641)	0.00939 (0.00906 - 0.00971)	0.22 (0.219 - 0.223)	0.175 (0.174 - 0.175)	0.0626 (0.0622 - 0.0641)	0.175 (0.174 - 0.176)	0.0981 (0.0959 - 0.0984)	9.71 (9.71 - 9.71)	5.75 (5.71 - 5.81)	0.128 (0.128 - 0.128)	0.4965 (0.4995 - 0.4995)
29-09-2020	1.17 (1.05 - 1.17)	0.986 (0.985 - 0.986)	0.00651 (0.00626 - 0.00923)	0.231 (0.23 - 0.246)	0.198 (0.197 - 0.2)	0.0496 (0.0489 - 0.0497)	0.205 (0.205 - 0.212)	0.113 0.113 0.115	8 (8 - 8.06)	6.99 (6.99 - 6.99)	0.0832 (0.0825 - 0.0833)	0.2285 (0.2155 - 0.2295)
06-10-2020	0.857 (0.856 - 0.859)	1.01 (1 - 1.01)	0.00489 (0.00466 - 0.00522)	0.21 (0.209 - 0.229)	0.175 (0.173 - 0.175)	0.0446 (0.0434 - 0.0447)	0.209 (0.209 - 0.216)	0.0919 (0.0916 - 0.092)	8.93 (8.93 - 8.93)	6.62 (6.58 - 6.76)	0.0869 (0.0866 - 0.0869)	0.29 (0.276 - 0.291)
15-10-2020	0.666 (0.665 - 0.665)	0.779 (0.778 - 0.778)	0.0526 (0.0527 - 0.0527)	0.217 (0.217 - 0.217)	0.399 (0.4 - 0.4)	0.0697 (0.0698 - 0.0698)	0.62 (0.61 - 0.623)	0.14 (0.14 - 0.141)	12.2 (12.2 - 12.3)	6.33 (6.33 - 6.33)	0.268 (0.268 - 0.268)	0.2655 (0.2655 - 0.2655)
22-10-2020	0.844 (0.844 - 0.844)	0.932 (0.932 - 0.932)	0.0283 (0.028 - 0.0312)	0.224 (0.223 - 0.223)	0.275 (0.27 - 0.275)	0.0831 (0.0821 - 0.0833)	0.474 (0.466 - 0.482)	0.213 (0.213 - 0.22)	11 (11 - 11)	6.37 (6.37 - 6.37)	0.27 (0.27 - 0.27)	0.37 (0.361 - 0.373)
28-10-2020	0.282 (0.277 - 0.277)	1.07 (1.07 - 1.07)	0.0304 (0.0303 - 0.0305)	0.259 (0.258 - 0.259)	0.237 (0.238 - 0.238)	0.0895 (0.0895 - 0.0898)	0.738 (0.667 - 0.765)	0.218 (0.217 - 0.221)	10.6 (10.6 - 10.6)	8.26 (8.26 - 8.26)	0.181 (0.181 - 0.181)	0.1135 (0.1135 - 0.1145)
04-11-2020	0.207 (0.107 - 0.247)	0.144 (0.0958 - 0.154)	0.105 (0.0808 - 0.121)	0.107 (0.104 - 0.109)	0.0292 (0.00209 - 0.0842)	0.182 (0.179 - 0.187)	0.039 (0.00116 - 0.166)	0.245 (0.242 - 0.254)	12.1 (12 - 12.1)	4.24 (4.17 - 4.35)	0.144 (0.117 - 0.252)	0.218 (0.104 - 0.2635)
08-11-2020
10-11-2020	0.529 (0.123 - 0.638)	0.133 (0.108 - 0.146)	0.358 (0.147 - 0.452)	0.136 (0.13 - 0.139)	0.0111 (0.000264 - 0.0817)	0.141 (0.114 - 0.191)	0.039 (0.00158 - 0.169)	0.241 (0.237 - 0.244)	12.4 (12.3 - 12.5)	3.44 (3.22 - 3.75)	0.473 (0.434 - 0.609)	0.2765 (0.214 0.3065)
17-11-2020	0.102 (0.102 - 0.102)	0.104 (0.103 - 0.104)	0.0926 (0.0926 - 0.0927)	0.107 (0.106 - 0.107)	0.0827 (0.0827 - 0.0827)	0.185 (0.185 - 0.185)	0.202 (0.2 - 0.202)	0.276 (0.274 - 0.276)	12.1 (11.9 - 12.2)	4.35 (4.35 - 4.35)	0.425 (0.425 - 0.425)	0.182 (0.182 - 0.1835)
24-11-2020	0.116 (0.116 - 0.116)	0.106 (0.105 - 0.106)	0.0738 (0.0738 - 0.0739)	0.109 (0.109 - 0.11)	0.109 (0.109 - 0.109)	0.191 (0.19 - 0.191)	0.402 (0.402 - 0.402)	0.212 (0.212 - 0.212)	12.8 (12.6 - 12.9)	4.44 (4.44 - 4.44)	0.492 (0.492 - 0.492)	0.189 (0.1885 - 0.189)
09-12-2020	0.181 (0.14 - 0.211)	3.72 (0.536 - 10.2)	0.177 (0.0984 - 0.244)	0.189 (0.165 - 0.232)	0.0506 (0.0244 - 0.0922)	0.156 (0.15 - 0.164)	0.0802 (0.00193 - 0.279)	0.0885 (0.0869 - 0.0907)	2.92 (2.48 - 4.46)	11 (10.8 - 11.2)	0.0911 (0.0896 - 0.0925)	0.094 (0.0915 - 0.098)
14-12-2020	1.29 (0.139 - 2)	5.63 (0.552 - 8.12)	0.103 (0.075 - 0.121)	0.195 (0.177 - 0.204)	0.00587 (0.000189 - 0.0462)	0.162 (0.16 - 0.166)	0.0513 (0.00115 - 0.175)	0.0701 (0.0602 - 0.0905)	3.6 (2.58 - 4.59)	10.6 (10.4 - 11.1)	0.0942 (0.0898 - 0.0963)	0.106 (0.0935 - 0.111)